https://vimeo.com/207299410
第一届网络社会年会 时间:2016年11月15日下午 地点:中国美术学院象山校区水岸山居会议室< 讲者:马修·傅勒(Matthew Fuller) 伦敦大学金匠学院文化研究和文化研究中心主任 译/卢睿洋 校译/黄孙权
首先感谢主办方的邀请。在信息量这么大、有趣讲者这么多的会议当最后一个发言者总是很难,很难回应。这两天我学到很多,得想想在会后怎么解压缩。思考有几位讲者提到深层的、不可见的运算问题,也是非常有趣的,不可见的世界还有其他层面。感谢各位工作人员对我的帮助。同时大会海报的设计也非常棒,它是可见的,但也体现了不可见的东西。
我想谈的某种程度上与许彬教授上一场所做刚好相反,他刚才巧妙地展现的是计算物件如何进入空间中,把空间用作某种隐喻,而我要讨论的是,计算的形式和结构如何具有一种特殊的空间维度的。所以,如果现实增强(AR)所做的是把空间当成界面的隐喻,把图形用户界面(GUI)拓展到城市中、世界中,把关系性范畴用于社交关系,那么我要思考的是计算系统中最最基础的元素如何变为城市的形式,这是我这次试图描述的。
[caption id="attachment_1218" align="aligncenter" width="666"]

哥德尔(Kurt Gödel)[/caption]
我想思考一下人们早期对计算的根基的研究,我们先看看哥德尔(Kurt Gödel)的工作,他是一位数学家。计算越发在实质上融入城市和社会的各种方式都包含了复杂丰富的文化意义。思考这些意义的一个方法是思考纹理(texture)问题。在一栋建筑中有大量纹理编织进建筑织物中,形成一种现代主义式对物质材料的整合的美学,这里有混泥土、泥浆、墙面,物料和空间的关系清晰可见,物质、纹理和空间性的互动产生了建筑。
我们也理解这样的系统,其中不同层面的采样率产生了时间值、颜色值等等、产生了反馈的系统。 我们把这些理解为文化形式。我认为,我们需要把这种理解植入计算形式中,而这在设计和艺术中已经非常发达的。我们要开始把计算的元素理解为富有文化意涵的,决定性的,它跨越了不同的文化实体。
这就意味着,必须把计算本身理解成文化,而不仅仅是一种技术的、功能主义的东西。我们目前对计算的描述已经开始认识到这一点,当然也不能止步于此,艺术家、设计师特别能把计算形式引向那种体现其文化价值和牵引力的方向。这样的理解的一个根基需要通过现代数学中的代数、信息论、拓扑学、集合论、逻辑,它们已经渗透进日常生活。这些数学形式在20世纪初浮现出来,而哥德尔是一个关键事件。
昨天我们已经讨论过同一性的问题,全喜卿教授和石田英敬教授的演讲都谈到了这个问题。同一性问题对于莱布尼兹的哲学以及对于他的哲学与数学的关系都是根本的。而不变的、本质的问题在这个背景下必须也改变了。
当计算进入外部世界,进入到社会、经济、城市的形式中,我们需要认识到计算形式(或者叫做数学的物质性形式)的同一性的多样性。
如果我们考虑网络,昨天已经从顶点边缘(vertex-edge)结构讨论过网络,而这些结构也可以被描述为表格、数组、可以被显示为有序数列,科霍宁图表(Kohonen graph)。这些都是网络的数据结构,它有独特的纹理,有自己的塑形方式,它有自己的交响乐,我们可以将它理解为文化的形式。
计算中还有另一种实体叫布尔逻辑(Boolean logic)。布尔运算以多种方式把真值表描述为通路和逻辑陈述,这些函数与结构控制有关,它们塑造着我们的城市。
逻辑命题、数学逻辑结构的纹理塑造了我们对城市的经验。尽管大会当中有很多讨论关于计算对人的影响,而我想退远一些,看看计算的影响如何形成空间,不只是计算对空间的影响,而是计算的空间形式。这就需要一种唯物主义的进路,它不仅要理解我们周边的物体、元素,还要理解数字、文字、概念也是一种物质形式,它们有自身独特的抽象等级。
我们正在经历这样的时期,社会进程、政治进程、美学进程都转译进了软件中,这些转译都基于在具有莱布尼兹式同一性的实体与符号序列或其他流程之间的等值兑换。这是如何发生的?社会关系如何变得可以被一系列的网络所标定,语言如何变得能描述出这些转型和它们需要的纹理?
这些图反映了机器学习的方式,这是另一种导出决策的网络结构。比如这个图是一个加权决策的编码。
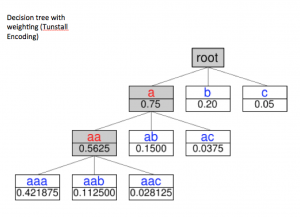
这是一个数值到另一个数值的映射,一个尺度到另一个尺度的过程。
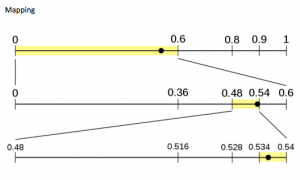
这里是把文件从一个格式转换到另一个的直线编程。
所有这些都应该被理解为文化过程。转变数据的模式,就像这个反馈系统所做的,这些都涉及到不同的纹理的生产,就像音乐中的音色被理解为发声的纹理,这些不同形式的编程、不同形式的数学转译,它们都有自己独特的纹理,这些都需要相应的文化分析和文化实践。在这个范围中,思考当代计算的形式也是很有趣的,我们往往认为那是同质的,但我和许煜一样认为其中有多样性。
这张列表来自哲学家史密斯(Cantwell Smith),它描述了计算的不同性质。每种性质都有自身独特的语法、句法、特殊的纹理和音色,它们产生了特定形式。它们的区别就像混泥土和陶土的区别一样,它们是不同的物料,我们使用它们的方式也不同。
但超出这张有限的清单,计算也和社会因素形成组合,比如官僚系统;或者美学因素,比如人们对游戏中渲染速度的要求,这些把计算的重点转移到商品化。同时,我们如果从不同的编程语言的角度追溯计算的历史,我们可以找到描述这些混合一体的问题的不同方法,比如冗余的美学;对功能或规则的强调;对与学习计算的有趣的环境或正式的方式的强调。
所以,我想提出的是,计算不是一个统一的实体,没有稳定的同一性,相反它是多变的、异质的,为了从文化上回应计算,为了与之工作,我们必须认识到这些,要看到有非常多不同类型的计算在运作。
但计算同样造成了文化本性的断裂,我们从一个基于文本的文化转向了一个基于符号程序的文化。但计算也拓展到了空间中,比如在克拉克(Andy Clark)的作品中我们能看到,计算已经进入了认知和经验中的具身、生成和生态的广泛维度。空间形式开始卷入心智的成形,我们也可以说心智的成形卷入了计算结构的成形中。
就着史密斯列表,我们还需要讨论比如映射、采样率、综合性的离散问题及其规则(离散性由这些规则确定)、同一性问题、不同的抽象模式、不同的计算形式如何导致了反馈问题、系统的自身性问题,构成噪音、干扰和增幅的语法的方式,什么样的姿势和信号能被识别的问题,什么被放大、什么被减弱。所以我试图通过哥德尔的工作来思考这些问题,以及从维也纳派解体后产生的这些数学形式如何导致了特定的计算式的文化产品。
1931年哥德尔的论文,在一个算术系统中,即使是算术的基本原则部分,也存在不能在系统内证明或反驳的命题(On Formally Undecidable Propositions of Principia Mathematica and Related Systems),处理了数学中的一致性问题。19世纪末20世纪初,问题在于“数学是否是一个完整的系统”,数学是否能产生关于自身的完整系统。对任何一个公理体系或试图构造一切数学的数学系统,哥德尔说,都存在系统之外的真数学陈述。所以有数学所产生的陈述无法在形式化的数学中得到证明。
也就是说,数学超越了自我一致的限制,它是一个生成的系统,当它拓展时,总是需要新的公理。数学在限制之中具有构成性的开放性,在这种状况下,数学逻辑层层叠叠,生长成一种临时的亚稳态,永远无法彻底总体化。这种状况现在被转译到计算的形式中,计算与更广阔的世界纠缠在一起并被改变。
所以哥德尔证明了,有可能产生真数学陈述,而无法被形式地证明。图灵继续对此做了精彩评注:它们不仅不能被形式地证明,我们甚至无法在有限的时间中说清它们是否能被证明。
没有一个公理系统足够充分以至于包含自身的证明。要做出证明,它就需要变成另一个系统的部分,而这又需要无穷的进一步形式化和公理的次系统。这意味着19世纪到20世纪成长起来的形式主义数学系统根本上崩解了。
哥德尔证明数学从根本上说是不完全的。根据数学史家杰里米·格雷(Jeremy Gray),这让数学从他所说的“机械证明的铁爪”下解放出来。所以,突然间数学就现代化了,就像现代艺术一样,它获得了自由。它可以是完全的实验性的、抽象的、思辨的、发明的实践,重新塑造了世界。
所以在数学中出现了结构主义运动:产生真理而不必与整个数学系统一致,但仍旧是生效的、构造世界的命题。这是今天的计算的基础。为了构造世界,它不必成一个完整的系统。
按照通常的理解,哥德尔的工作划清了为真与可证。但我对这部分并不十分感兴趣,它根本上对数学有意义,而我更感兴趣哥德尔的工作对数学之外的世界的意义。哥德尔描述了转译规则,由此一个数学领域可以映射到另一个。他的目的是推敲不可决定性和形式系统之内/之间的悖论。哥德尔以罗素(Bertrand Russell)( BRussell)和怀特海(Alfred North Whitehead)(ANWhitehead)的著作《数学原理(The Principia Mathematica)》为例,说“从形式的角度看,证明无非是有限的公式序列”,形式系统中的每个证明或陈述都可以被简单符号比如数字的序列所映射。系统扩展一次,证明数组的形式就复杂一层,成为公式序列的序列。相应地,关于系统的命题将用系统所能提供的方式来描述。这一“相应地”,意味着任何形式化系统都能在映射过程中转译为另一个具有更高或更低精确性的系统。然而,这一可映射性基于一下认识:系统在形式上是不完全的;在不同尺度间的转译和不同集合之间的合取都可能包含悖论。
哥德尔的成就在于,他找到了创造递归过程的方式,用一个代码配置一个命题,而命题本身也是一个代码;他将不可计算性系统化,也就是说为处理、认识数学中的活的空提供了方法,甚至是整合了空。他的目标是处理数学中的不完全性,而这个系统在整合不可通约性时发挥了巨大作用。
这个系统根本上说是不连续的,其中有大量的空,但仍旧是系统化的。这正是哥德尔提供的作为当代文化形式的计算所具备的能力:既是不连续的、充满空点,能产生大量活的空,同时又能被系统化。这就是我们所认识和处理的作为文化形式的计算。
哥德尔所描述的一个例子,后来在计算中被成为“数据结构”,它处在每个数学命题与它的元数学检验系统之间的关系之中。建立另一种映射,将与维特根斯坦所说的有关:从一种语言游戏(一套符号程序)移到另一种。哥德尔的工作也促成了香侬( Claude Shannon)与韦费尔(Warren Weaver)工作,他们建立了信息论,后来成为通信理论的基石,通信理论描述这样的图表。
我感兴趣的就是这样的结构如何构成数据结构的基础。哈尔平之前提到的冒泡排序描述的就是处理列表的不同的方式。我认为每种排序方式都有其自身的美学和编舞。这种把数字在列表中混合、分离编舞的方式,都深刻地体现出文化特性,其中有加速、减速,建立了实体之间的各种关系。
哥德尔以一组符号序列来定义另一组代码序列,以此在处理数学问题时获得高度的抽象,而这种高度抽象反过来又成了计算对我们的世界进行操作的方式。
这是一个纯数据中的简单补丁制作器。这是早期用于登记的电话语音编码的控制论技术,是处理电子信息的登记技术,这是语音编码器。哥德尔的工作导致的结果之一,便是这种对陈述的编码,用别的代码来编码数值。
语音编码器的发明者之一维纳(Norbert Wiener)也看到哥德尔的研究的普及化可能,由此思考比如声波的数值如何被编码,造成了普遍的对数值进行编码。维纳所谈论的是将感官输入通过语音编码器转换成另一种感官输出的系统。大家也许对语音编码器最近在自动调解系统系统的应用会比较熟悉,歌手用它来让自己的声音听上去有点电磁感。维纳看来,四十年代发明的声音编码技术可以把感官信号从一套器官转译到另一套。
他说,通过这些编码,“我们把大脑皮层中的部分功能转移到了人工的外部的皮层上。我们的做法是在语音编码器中把各种语音频段分离开来,调节它们的震动频率以便让触觉易于分辨,再把这些调整后的不同的频段传输到在空间上分离的可触区域。比如五个频段对应五个手指。” 这某种意义上是一种现实增强技术,跳过视觉直通触觉,比如使用舌头。
这是另一个系统,由神经学家利塔(Paul Bach-y-rita)发明,他沿着哥德尔和维纳的思考,关注神经的可塑性与编码问题的关系。根据这个研究分支,如果任何事物都能被编码,那么神经系统的不同部分也就能被解码和再编码。
然而,编码的普遍化还有其他后果。当每条代码都能被多种其他代码解释,理解这个状况的一个重要途径是精神分裂。精神分裂在这里的含义是:系统中的不可通约的符号和运作的双重性或多重性导致了编码和解码的问题,这个系统具有明示的符号和公理,但其中的符号和运作却在其他的、多重的尺度上运作。我们已经讨论过当代政治中的精神分裂,私领域的编码系统、私仇或轻微的冒犯被放大到国家的尺度,川普就是极端精神分裂的总统。他对当代世界毫无遮拦的力比多式憎恨杯放大到了国家政治的层面。这就是编码和尺度的问题,根本上也是围绕编码问题的现代性的问题,在数学的意义上,这是同一性的意义和同一性的丧失的问题。同一性的丧失,是身份的丧失的根本原因,而川普想要以种族主义的、性别化的系统来恢复身份。
我们看到,同一性意义的丧失也反映在艺术中,抽象表现主义试图在画布上映射身体的情感和感觉,直接映射符号系统(功能主义也以不同方式试图达到这个目的)。我们也可以说,这种多义性状况,这种编码、解码的精神分裂,就本身而言并非新情况。它也被各种美学趋势所实践,如象征主义、精神分析、训诂学和解释学。这些是人文领域的基础工作,由此可以来思考编码和解码的问题。
所以这些被哥德尔的工作整合起来的过程(展开为一种计算的现实)以及精神分裂的普遍化(它由编码系统通过其他符号,比如资本主义的符号,映射到其他评价系统中所导致)都应该在人文、艺术领域被说明,这些领域在介入那些空间时有其独特的权力和位置。
这就意味着我们需要理解类似这个矩阵一样的系统,其中不同的数值形式被交差转译、相乘。逻辑系统和数学序列互动,从而产生复杂的变体形式。石田英敬教授的演讲中提到过塞尔(Michel Serres)的一本著作《赫尔墨斯III. 翻译》,是我们理解数学与历史,数学与沟通系统之间的运动的工具箱。
编码、解码系统中存在大量的形式化,这些系统一般而言是总体化的,但又存在不连续,不同形式的语法、语义在不同的尺度上互动,一方面为了维持系统的一致性,它们必须公理化,不管它们多么精神分裂;同时它们大量地应用在当代社会中,看上起是一个操作系统在运行,它之下还有其他系统,或许多社会操作系统在同时运行。这种精神分裂的状况是当代社会的权力,这也意味着计算具有了重塑社会和美学形式的巨大能力。
这种改变社会和美学形式的语义的能力是计算形式的行动语法,是社会的巨大可塑性以及计算文化的政治经济形式的巨大潜能的条件。这种条件的政治要点的是认识到这种可塑性,理解在社会、美学和经济的角度,这种可塑性意味着什么,并且运用它。
与塞尔的工作相比,哥德尔的工作完全处在数学逻辑的瞬时中,公式在被构成的时刻就被执行了。而塞尔所带来的是,一个公式如何转译到另一个,数学的公式如何转译到社会、城市、文化和哲学中的问题。在不同的历史时刻,映射的条件、限制或语义也不同,转译本身的规则也在转变。
许煜也提到了赫尔墨斯,沟通之神,某种意义上也是公共之神,但根据塞尔的著作,它还是捣蛋鬼,总是引入噪音和恶作剧,所以我们可以说它特别值得艺术家和设计师学习。计算开启了转译、映射技术的普遍化,我们可以在多种领域中看到转变。
哥德尔在数学中应用的映射方法展开在城市的形式中;哥德尔引入的转码方式也造成了数学系统、符号系统的精神分裂,这是一种拜占庭式的过程,也就是说事物总是在不同层面上运作,可以从不同层面上解释,这增加了解释的焦虑。如果事物都在多个层面上编码、解码,这也意味着我们已然生活在信息走私、程序走私的时代。有大量的事物在多尺度上运作,两周前我们看到分布式拒绝服务攻击(DDOS attacks)的大平台变成了简单的网络摄像头,相应的,民主变成了选出煽动家的拜占庭式系统。我们必须在这种编码、解码的精神分裂式的层次中理解计算的功能。
在这个由哥德尔所创立、由计算所布置的状况中,映射可以在不同相关领域间产生,它们根本上是不完全的,具有重叠和多形式的可能性,有可能在多个层面上同时投射计算的、社会的、美学的、城市的和政治的形式。
我想提出的是,在这种情况下,城市结构开始与计算中的数据结构结合、转码。之前我已展示过数据结构的图表形式,其中包含多种网络类型,比如数组、列表、表格、矩阵、栈、堆等等。所有这些数据结构类型都具有特殊的空间性质,它们的命名都有空间隐喻,这并非偶然。
历山大·勃洛克(Alexander Blok)的著名诗篇“夜,街,灯,药店”,正描述了一条街道的基本组成,就像一个列表。数据结构可以是层级式的,如树形的、目录型的、序数的或按字母次序的,也可以是非层级的形式,比如堆、试算表或关系型数据库。
不同的程式语言包含特殊的能力来处理特殊类型的数据结构,比如递归列表。但每种数据结构都有其特殊的政治,比如一个有限的列表,只有特定的实体的数字才能置入其中,某些事物则被排除在外。我们都熟悉排序的政治和堆栈(stack)政治。
数据结构中有计算选择,按这种选择,数据结构系统对数据进行编码,形成结构和秩序。这些结构固有自身的美学,它们也与不同的诗的形式有关。
而大数据的观念是,通过引入海量无结构数据、无定形结构,消除数据结构,以此顺应这些数据多形态的性质。但应该说,这种情况下数据结构接近神经网络或机器学习结构。所以,大数据和机器学习并没有把数据结构从计算中清除,数据结构只是移动了位置,改变了其形式条件,而这一形式条件是我们需要理解的。
最后我想提一提法国作家乔治‧佩雷克(George Perec)六十到八十年代的作品,他于九十年代去世。
就着勃洛克的诗作,我们要考虑下,什么是城市的原本结构。就数据结构成为城市结构,我想我已经展示了数据结构根本上是空间性的,但还需要思考原本的数据结构源自城市。
这是一本很小的册子,一本程序手册《穷尽巴黎的一个地点的企图(Attempt at Exhausting a Place in Paris, (1975))》,他描述了如何坐在咖啡馆里,标注过往行人,快速找出他们的服饰、行为的模式。他在巴黎的一个特殊地点实施了计划,发展了一种对日常生活的非个体过程的系统性映射。
另一本书《空间的种类(Species of Spaces)》1974年被翻译成英文,在书中他继续了这种方法,直到九十年代。他试图找到描述不同尺度的空间特质的方法,从一页书到一张床,到一间房到一条街,到邻居、到城镇、到乡村、到国界、到大陆。
这个计划要发展一种对空间的独特功能的理解,他将这种功能称为““日常之下”(Infra-ordinaire)”,它们处在我们感知层面之下,却结构着我们的日常现实,它们如此普通以致于我们无视它们。 由此可以结合大会中我们对算法的批判。
我之所以想要联系佩雷克、联系哥德尔,是因为它们都描述了形式系统,这些系统都以不同的方式是空间性的。哥德尔的系统处理的是数学的编码,之后扩展到数据结构和一般的代码和编码问题;而佩雷克的系统在于发现被我们的日常感知层面忽略的事物,它们在我们的日常经验中获得形式牵引力,而我们却不知不觉。这两个系统都是我们理解当代生活中计算的纹理的途径。
谢谢各位!
[slideshare id=72409349&doc=matthewfullercitydatastructure-170221125444]
