Privasi sebagai Barang Publik
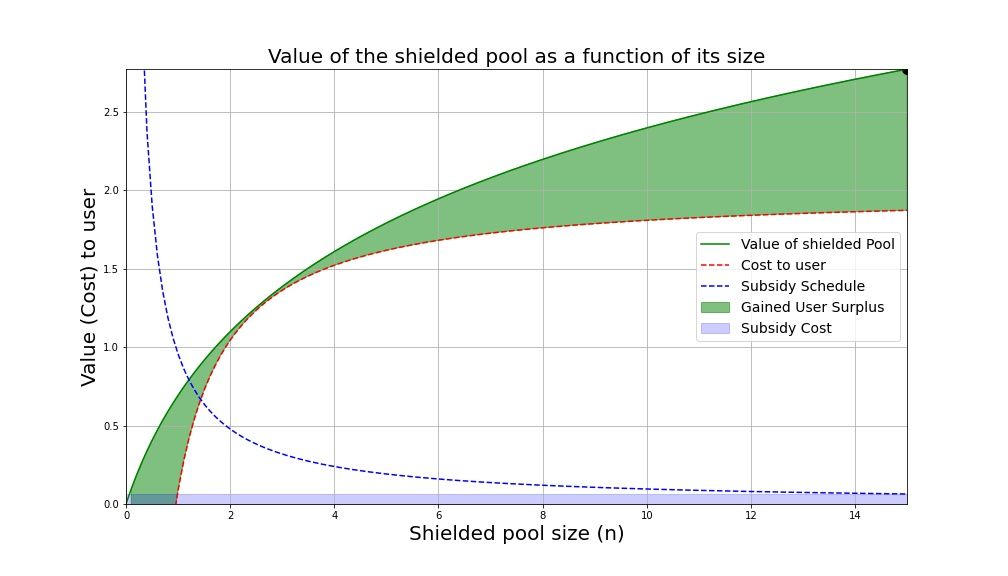
Di Namada, shielded set disubsidi, sehingga pengguna awal tidak bergantung pada keberadaan shielded set yang cukup besar. Sebaliknya, subsidi diprogram untuk memastikan bahwa berapa pun besarnya shielded set, terdapat insentif yang cukup bagi aset untuk memasuki shielded set.
Dalam ilmu ekonomi kontemporer, suatu barang diklasifikasikan sebagai barang publik jika barang tersebut non-rivalrous dan non-excludable . Sederhananya, suatu barang dikatakan non-rivalrous jika konsumsinya oleh satu orang tidak menghalangi konsumsinya oleh orang lain. Suatu barang disebut non-excludable jika konsumsinya tidak dapat dicegah oleh siapa pun setelah barang tersebut ada.
Contoh barang publik termasuk mercusuar, lampu lalu lintas, sistem peradilan yang berfungsi, teknologi sumber terbuka, gagasan publik, sanitasi, dll.
Sebenarnya, privasi itu sendiri bukanlah barang publik karena meskipun tidak bersifat persaingan, privasi tetap dapat dikecualikan. Mencegah pengguna memasuki shielded pool adalah hal yang sepele (secara hipotesis, Namada tentu saja tidak memiliki izin). Namun, hal tersebut tetap menunjukkan sifat yang umumnya diasosiasikan dengan barang publik, yaitu memiliki eksternalitas positif. Hal ini terjadi ketika konsumsi suatu barang bermanfaat bagi orang lain, dan eksternalitas positif ini memang tidak dapat dikecualikan. Lebih konkretnya, ketika satu pengguna memasuki shielded pool, hal ini meningkatkan privasi total untuk semua orang yang sudah berada dalam kumpulan terlindung, dan tidak mungkin mengecualikan siapa pun yang sudah berada di shielded pool untuk mendapatkan manfaat darinya.
Eksternalitas positif dapat dijelaskan dengan contoh mainan (dan diagram yang menyertainya).
Demi kesederhanaan, asumsikan setiap “agent” dalam perekonomian adalah identik dalam hal preferensi mereka. Kami berasumsi bahwa pengguna menghargai peluang untuk berada dalam kumpulan privasi, dan bahwa nilai kumpulan privasi meningkat seiring dengan bertambahnya ukuran kumpulan privasi. Sepele, kumpulan privasi yang terdiri dari 0 orang tidak ada artinya. Lebih lanjut, kami berasumsi bahwa setiap peningkatan tambahan dalam ukuran kumpulan privasi memiliki properti "penurunan manfaat marjinal", dalam arti bahwa setiap pengguna tambahan berkontribusi lebih sedikit terhadap keseluruhan privasi secara keseluruhan. Ketika kumpulan privasi (privacy pool) semakin besar, manfaat tambahan jika seseorang memasuki kumpulan (pool) tersebut menjadi dapat diabaikan. Dalam ilmu ekonomi, kita cenderung merepresentasikan hal ini melalui fungsi "utilitas", yang ada untuk mengukur biaya dan nilai bagi agent. Pilihan wajar untuk fungsi utilitas yang menunjukkan sifat-sifat di atas diberikan oleh
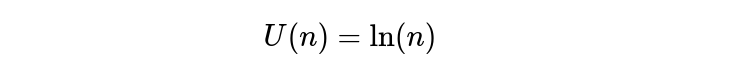
Di mana n adalah ukuran set privasi. Meskipun ini bersifat diskrit, untuk mempermudah, kami akan bekerja dalam domain kontinu.
Selain itu, kami berasumsi bahwa terdapat "biaya" (sebut saja C) yang tidak dapat dihindari bagi pengguna untuk memasuki set privasi. Di dunia nyata, hal ini dapat berhubungan dengan pembelajaran tentang kriptografi tanpa pengetahuan, penanganan kunci pribadi, dan bentuk "usaha" serta risiko lain yang mungkin diambil pengguna sepanjang perjalanan. Seperti yang dikemukakan Gavin Birch, ada juga biaya peluang jika tidak meminjamkan aset atau mempertaruhkan aset dalam sistem yang transparan. Mudah-mudahan suatu hari nanti kita dapat menemukan cara untuk melakukan hal ini dalam shielded set juga.
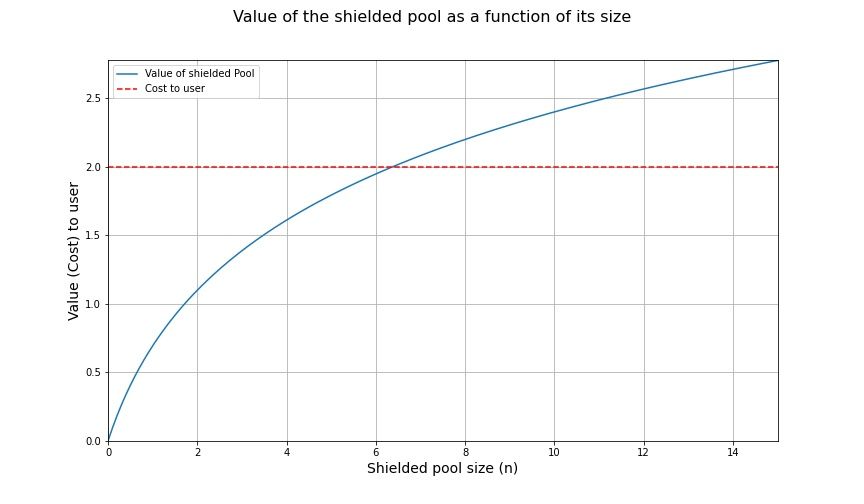
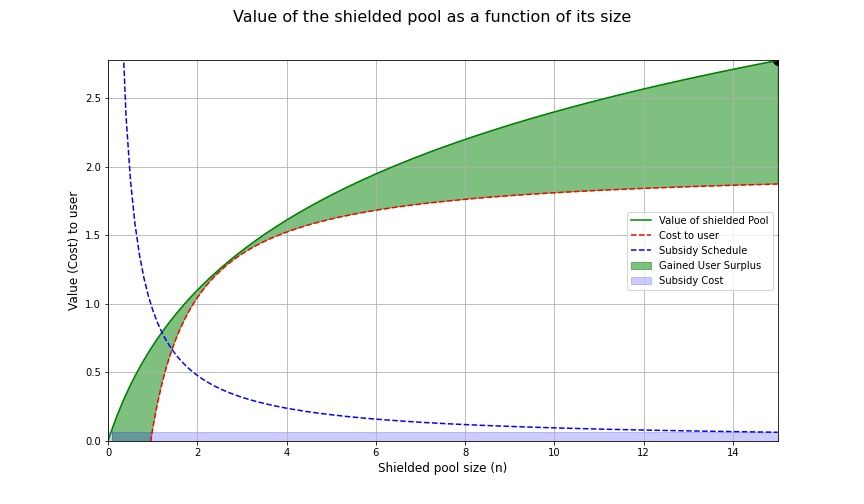
Karena eksternalitas positif yang terkait dengan memasuki perangkat privasi, ada “nilai yang belum direalisasikan” yang hilang dalam perekonomian jika pengguna tidak dapat berkoordinasi. Meskipun tidak ada pengguna lain yang termasuk dalam kumpulan privasi, nilai kumpulan privasi adalah 0. Dalam perekonomian kontemporer, "nilai kumulatif yang hilang" ini (dijumlahkan dari semua pengguna dalam perekonomian) disebut sebagai Kerugian Bobot Mati (Deadweight Loss). Kerugian Bobot Mati divisualisasikan di bawah ini melalui area yang diarsir antara nilai dan biaya individu untuk masuk.
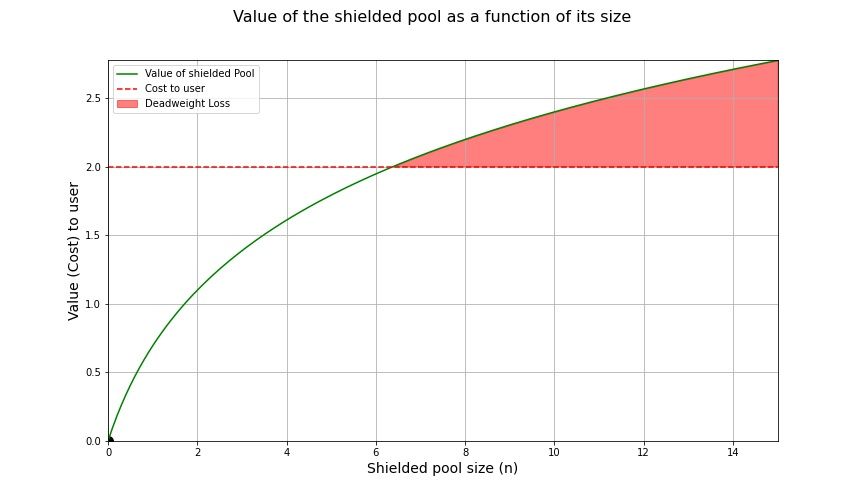
Oleh karena itu, jika protokol dapat memberikan insentif kepada sejumlah pengguna (dengan ukuran aset yang besar) untuk memasuki kumpulan privasi (privacy pool) sehingga terdapat nilai yang cukup untuk tetap berada dalam kumpulan privasi, maka masalah koordinasi akan terpecahkan. Jika "social planner" memiliki pengetahuan penuh tentang jumlah pengguna yang dibutuhkan untuk mencapai nilai "tipping-point" ini nilai n⋆, ia dapat menawarkan jumlah subsidi yang tepat untuk memberi insentif pada subsidi pertama n⋆ pengguna untuk menggunakan protokol dan tidak lebih.
Kami menyarankan pendekatan alternatif, dimana kami dapat mengklaim bahwa:
Jika subsidi s(n) berbanding terbalik dengan ukuran shielded pool, misalnya:
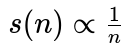
maka untuk konstanta proporsionalitas yang cukup besar k, subsidi akan memberikan insentif kepada jumlah pengguna yang tepat untuk bergabung dengan sistem. Selain itu, skema insentif ini mempunyai manfaat tambahan karena sifatnya yang terbatas dan dapat diprediksi . Ini bukan satu-satunya solusi yang mungkin, namun merupakan salah satu solusi dan tampaknya wajar.
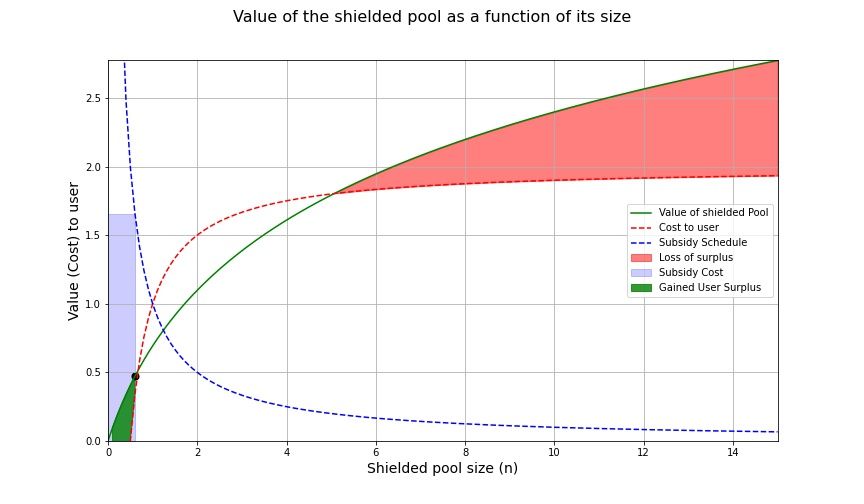
Subsidi di atas tidak cukup dalam memberikan insentif kepada pengguna untuk bergabung dengan jaringan, meskipun subsidi ini sedikit menurunkan ambang batasnya. Dalam contoh di atas, ukuran kumpulan privasi akan meningkat dari 0 menjadi ~0,6. Untuk mencapai masa kritis ini, kita perlu memberikan insentif untuk perangkat privasi dengan ukuran minimal n ≈ 5.4
Jika kita meningkatkan insentif agar sebanding dengan biaya yang ditanggung pengguna, itu sudah cukup. Keuntungan tambahan dari perancangan subsidi dengan cara ini adalah bahwa subsidi dapat dengan mudah diinterpretasikan, total subsidi sama dengan biaya yang harus ditanggung oleh setiap pengguna, yang didistribusikan ke semua pengguna.
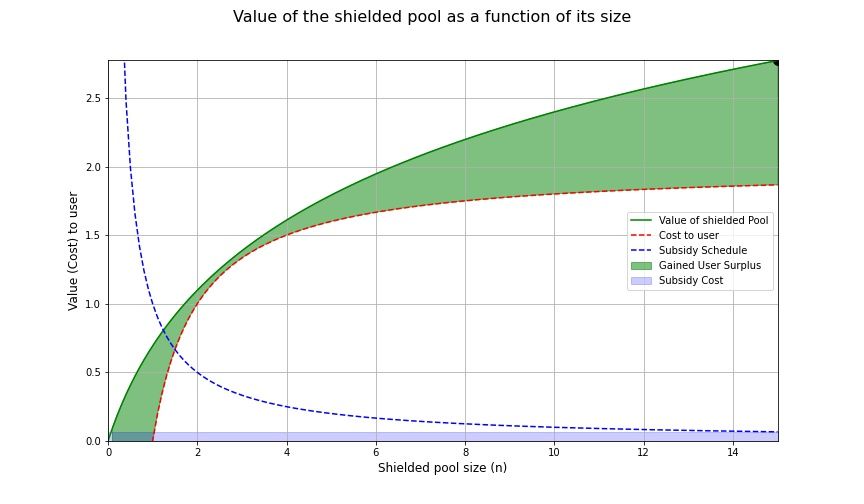
Kini titik minimalisasi area antar kurva diberikan oleh titik di mana biaya yang ditanggung pengguna (setelah subsidi diperhitungkan) bersinggungan dengan nilai kumpulan terlindung. Tantangan: Dapatkan ini!
Petunjuk: pikirkan tentang meminimalkan luas dan turunan dari suatu integral menjadi kurva itu sendiri ...
Yang membawa kita ke:
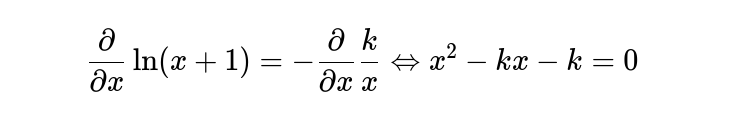
Kita juga perlu memastikan bahwa kedua kurva tersebut memiliki tepat satu titik perpotongan. Yaitu
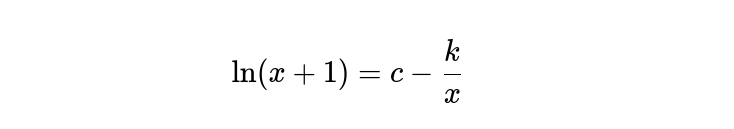
Kedua persamaan simultan ini dapat diselesaikan k∗
Hal ini meminimalkan biaya subsidi, dengan mengorbankan interpretasi yang rapi
Kesimpulan utama dari artikel ini adalah bahwa memasuki shielded pool memiliki eksternalitas positif. Tanpa subsidi, akan timbul masalah koordinasi yang berulang. Pengguna ingin memasukkan set terlindung yang cukup besar. Namun, shielded set tidak dapat terwujud karena keberadaannya bergantung pada aset yang masuk ke dalam set terlindung sejak awal.
Dengan adanya subsidi, pengguna awal tidak bergantung pada keberadaan perangkat terlindung yang cukup besar. Sebaliknya, subsidi diprogram untuk memastikan bahwa berapa pun besarnya kelompok yang dilindungi, terdapat insentif yang cukup bagi aset untuk memasuki shielded set.
Selain itu, dengan asumsi yang masuk akal, subsidi yang dibangun dengan baik mempunyai beberapa manfaat. Total biayanya terbatas , tidak bergantung pada ukuran perangkat yang dilindungi, dan dapat diprediksi sepenuhnya. Lebih lanjut, hal ini memberikan nilai sosial yang tidak terbatas (hanya terbatas pada ukuran total seluruh aset di dunia). Akhirnya solusinya dimana k = c cukup mudah untuk diterapkan sehingga persamaannya dapat dipahami oleh siswa sekolah menengah.
Untuk masukan dan komentar, silakan kunjungi topik terkait di forum Namada .
Saya ingin mengucapkan terima kasih kepada Gavin Birch dan stellarmagnet atas komentar mendalam mereka sejauh ini
