
Trilemmas suck
By choosing any two points on a pick-2 triangle, you are neglecting the third. Another schoolyard example is the tradeoff between looks, relationship status, and sanity. Sane, good-looking people are always in a relationship. If you spot a handsome, single person – so the joke goes – you might want to keep your distance.
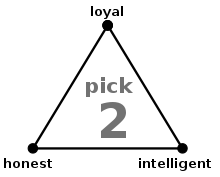
A more professional example is the CAP theorem, which is a tradeoff between characteristics of a data storage system. The three choices are Consistency (C), Availability (A), and Partition (P) tolerance. All good things to have, but you can only have two. The lonely, abandoned letter which you did not pick will define your system’s Achilles Heel.
Here are some other inconsistent triads:
As mentioned in all of these examples, three-body problems are basically insoluble. You can’t have your cake and eat it too. But each of the authors of these triads also noted a workaround. The consequences of your pick-2 can be mitigated by cycling or multiplexing, depending on the trilemma and who is trying to solve it.
Single triad games, played once, will always neglect one element. Multiple plays allow for fragility to be mitigated by cycling which two points you pick. This means you won’t accumulate a critical weakness over time. Parallel runs, usually done by networks (of people or devices) can do the same by making a balanced mix of choices, i.e. multiplexing.
Pythagoras rides a bike
Once I heard a comedian talking about dualism and our tendency to see everything as binary or part of a two-ended spectrum. Maybe, like he said, this compare-and-contrast attitude comes from the fact that we have two hands, two feet, two eyes, and so on. We are physically divisible by two (ish).
Following this logic, octopi would be extremely lateral thinkers. It also follows that we should seek a three-armed animal to mimic. But, since my background in natural sciences is a bit shoddy, I’ll visualize this model with a Dr. Seussian bicycle.

While extraordinarily janky, this bicycle does function. It does so thanks to its wheels being shapes of constant width. Circles, too, fall in this category. What makes these shapes special?
When they are wedged between two parallel lines, the diameter is constant, no matter which way the shape is rotated. These triangular wheels are called Reuleaux Triangles. They are also used in combustion engines as a more efficient alternative than a piston.
Inconsistent triads can be “solved” by cycling. If the mapped tradeoff is a triangle, cycling will work. If it is a square, or if you have more than three points to balance, you will need to adjust your suspension.
Just move around, young padawan
With these triangular tires (Coasean Trilemmas) it’s essential to cycle your tradeoffs. The main symptom of tradeoff lock-in is a sense of feeling stuck. This is sometimes called spinning your wheels. You might feel like you’re cycling, but you’re really not. You’re bobbing up and down. You’re breaking a sweat. But you’re not going anywhere.
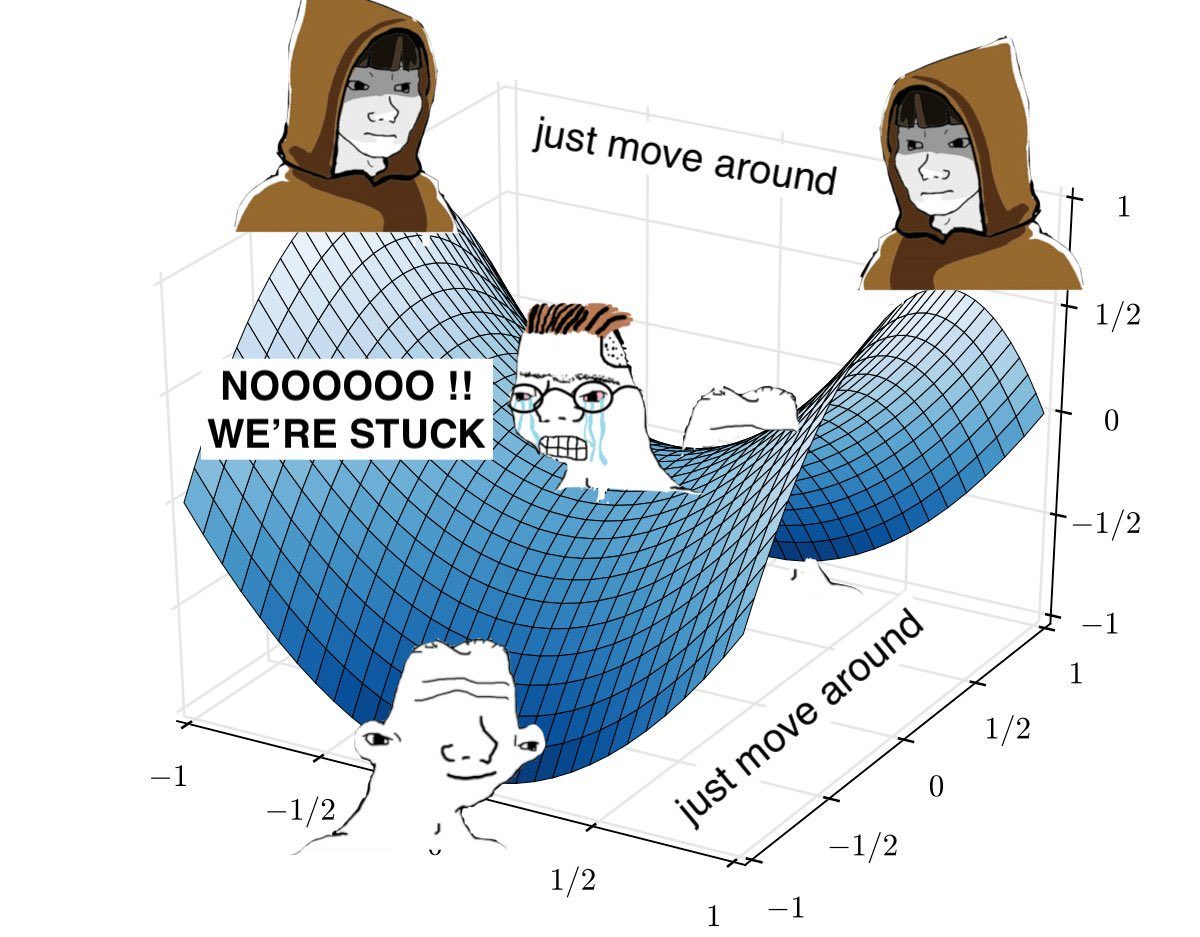
Continuing the metaphor of the triangle-wheeled bike: the first necessary component of this bike is the nature of its wheels. It basically functions like a circle. You might have also noticed the strange rollers sitting above the wheels. Those spin as the bike moves, forcing the suspension to respond uniformly, and thereby ensuring that the full surface of the tyre is used.
This will get out of hand (and outside of my mediocre engineering acumen) soon. So, I’ll stop analogizing here. The point is relatively simple. Inconsistent triads are everywhere. So we’re constantly juggling these kinds of tradeoffs. And there’s a good and bad way to approach them.
Pick a lane, Lance Armstrong
The so-called “middle path” is not a solution. Just like when you’re facing a pareto problem – if you take the average of two components of a solution, you’re left with crap. Someone prepping for an athletic competition will spend the vast majority of their training doing light work. Only 5-20% will be intense, high performance work. If a marathon runner ran marathons every day, they’d burn out. If they only went for 5 km runs, they’d lose their race. If they ran 30 km every day, they’re at risk of burning out and losing.
Same goes for trilemmas, but to an even greater extent. Attempting the middle path exposes you to more weaknesses and doesn’t allow you to accrue enough benefits. There might be some mathematical expression I could use to illustrate this, but I’m really not that great at math… So I’ll wait for someone else to do that.
The suggested approach of cycling is ubiquitous across all fields where I’ve seen inconsistent triads crop up. These solutions have slightly different flavors depending on the setting.
Soft vs. Hard Cycling
Trilemmas in the built environment are harder to solve than behavioral trilemmas. This is simply a problem of fixed costs. A nuclear power plant trying to choose between safety, efficiency, and cost is not going to be able to rebuild the facility every year to cycle their triangle.
Networked vs. Individualized Cycling
Groups have one pronounced advantage when it comes to Trilemmas. It’s easier for them to spread strategies across a tradeoff space. If members have a properly diversified mix, then the group will perform better. Individuals have less capacity to do this, generally speaking, and have to rely on repeated iterations. Spreading is not as viable a strategy, since there are simply fewer options available. But, individuals have fewer coordination costs.
Repeated games vs. One-offs
For each trilemma, how often you have to choose between the points differs. Weick’s example of theory types is a choice that a researcher would have to make each time they write a paper. When a power plant is built, there is a choice between cost, safety, and speed. But researchers write many more papers than engineers design power plants. Trilemmas are little games – the more frequently you play, the better cycling will work as a strategy. Networked cycling works in a similar way – multiple actors facing the same tradeoff can multiplex, even if each actor in the group only plays once.
A footnote on Karmic Oscillation, The Wheel of Time, Kali Yuga, and other B.S.
Many people believe that history repeats itself. That there is a hidden wheel behind the plot, cycling us through each stage again and again. Who knows, who cares. Cycling is a tool for mitigating critical weaknesses, not predicting the future.
